Disclaimer: this a more technical post that requires some prior knowledge of how ZK proving systems like Halo2 operate, and in particular in how these APIs are constructed. For background reading we highly recommend the Halo2 book and Halo2 Club.

A common design pattern in a zero knowledge (zk) application is thus:

• A prover has some data which is used within a circuit.
• This data, as it may be high-dimensional or somewhat private, is pre-committed to using some hash function.
• The zk-circuit which forms the core of the application then proves (para-phrasing) a statement of the form:

“I know some data D which when hashed corresponds to the pre-committed to value H + whatever else the circuit is proving over D”.

From our own experience, we’ve implemented such patterns using snark-friendly hash functions like Poseidon, for which there is a relatively well vetted implementation in Halo2. Even then these hash functions can introduce lots of overhead and can be very expensive to generate proofs for if the dimensionality of the data D is large.

You can also implement such a pattern using Halo2’s Fixed columns if the privacy preservation of the pre-image is not necessary. These are Halo2 columns (i.e in reality just polynomials) that are left unblinded (unlike the blinded Advice columns), and whose commitments are shared with the verifier by way of the verifying key for the application’s zk-circuit. These commitments are much lower cost to generate than implementing a hashing function, such as Poseidon, within a circuit.

Note: Blinding is the process whereby a certain set of the final elements (i.e rows) of a Halo2 column are set to random field elements. This is the mechanism by which Halo2 achieves its zero knowledge properties for Advice columns. By contrast Fixed columns aren’t zero-knowledge in that they are vulnerable to dictionary attacks in the same manner a hash function is. Given some set of known or popular data D an attacker can attempt to recover the pre-image of a hash by running D through the hash function to see if the outputs match a public commitment. These attacks aren’t “possible” on blinded Advice columns.

Further Note: Note that without blinding, and with a sufficient number of proofs, an attacker can more easily recover a non blinded column’s pre-image. This is because each proof generates a new query and evaluation of the polynomial represented by the column and as such with repetition a clearer picture can emerge of the column’s pre-image. Thus unblinded columns should only be used for privacy preservation, in the manner of a hash, if the number of proofs generated against a fixed set of values is limited. More formally if M independent and unique queries are generated; if M is equal to the degree + 1 of the polynomial represented by the column (i.e the unique lagrange interpolation of the values in the columns), then the column’s pre-image can be recovered. As such as the logrows K increases, the more queries are required to recover the pre-image (as 2^K unique queries are required).

The annoyance in using Fixed columns comes from the fact that they require generating a new verifying key every time a new set of commitments is generated.

Example: Say for instance an application leverages a zero-knowledge circuit to prove the correct execution of a neural network. Every week the neural network is finetuned or retrained on new data. If the architecture remains the same then commiting to the new network parameters, along with a new proof of performance on a test set, would be an ideal setup. If we leverage Fixed columns to commit to the model parameters, each new commitment will require re-generating a verifying key and sharing the new key with the verifier(s). This is not-ideal UX and can become expensive if the verifier is deployed on-chain.

An ideal commitment would thus have the low cost of a Fixed column but wouldn’t require regenerating a new verifying key for each new commitment.

Unblinded Advice Columns

A first step in designing such a commitment is to allow for optionally unblinded Advice columns within the Halo2 API. These won’t be included in the verifying key, AND are blinded with a constant factor 1 – such that if someone knows the pre-image to the commitment, they can recover it by running it through the corresponding polynomial commitment scheme (in ezkl’s case KZG commitments).

If you’re familiar with the Halo2 API the pseudo code for this is akin to

for (column_index, advice_values) in &mut advice_values.iter_mut().enumerate() {
    for cell in &mut advice_values[unusable_rows_start..] {
                    *cell = Scheme::Scalar::random(&mut rng);
                    if witness.unblinded_advice.contains(&column_index) {
                        *cell = Blind::default().0;
                    } else {
                        *cell = Scheme::Scalar::random(&mut rng);
                    }
                }
            }

Now that we have a commitment that can be consistently reproduced given a known pre-image – where do we put it within the plonkish grid of Halo2?

Grid Engineering

In the proof transcript that Halo2 produces, the commitments to the advice columns are the first serialized elements. Further these points are serialized in the order in which the advice columns are initialized.

To avoid having to do complex indexing later on (see next section), we want to put the values that are being committed to in the first columns of the plonk grid.

Say we’re committing to 3 separate datum, D1,D2,D3 we’ll want to assign each of these to the rows of the unblinded advice a1,a2,a3.

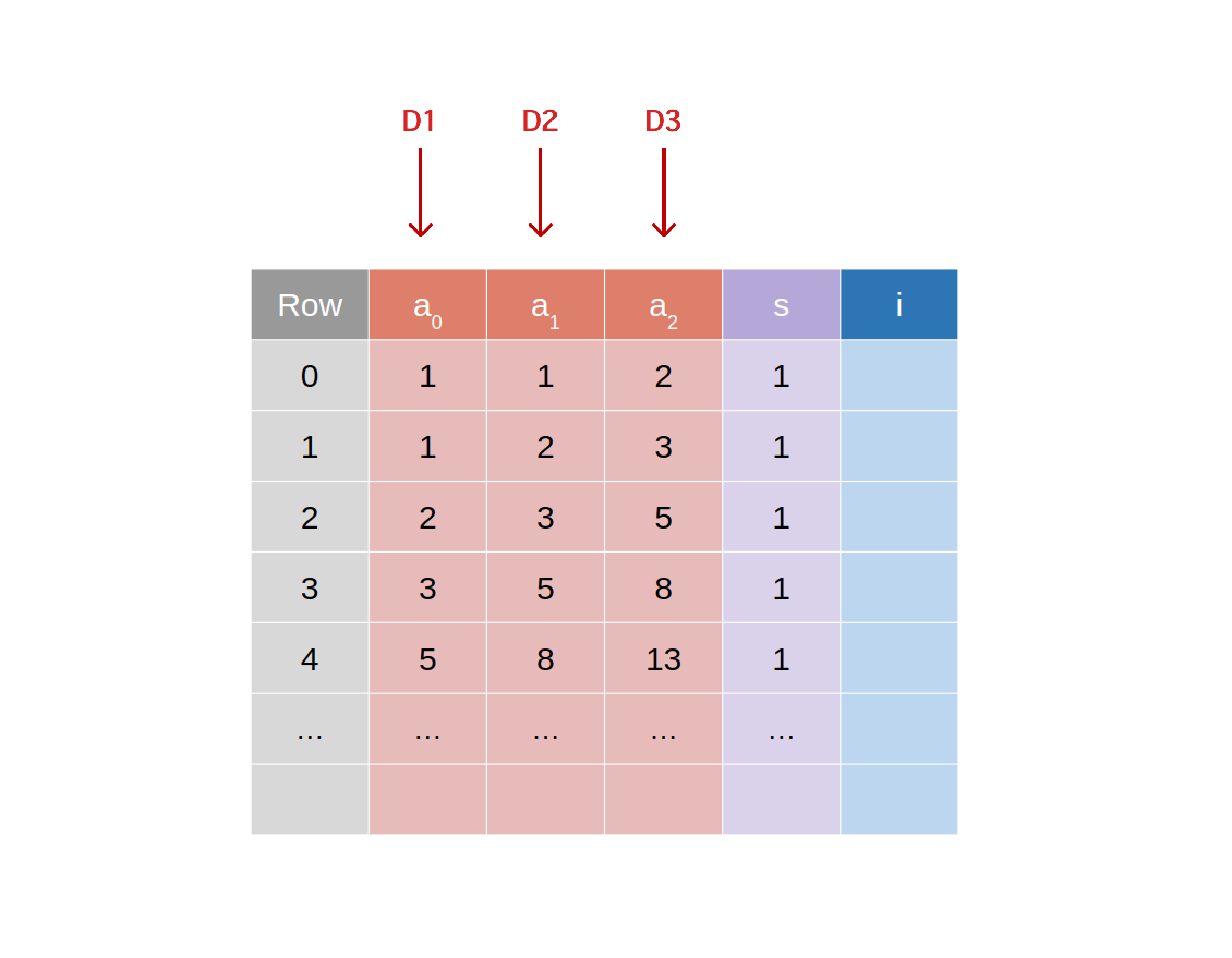
The proof transcript is then generated and the affine projections of the curve points that correspond to the commitments to D1,D2,D3 are its first elements.

Given these commitments don’t correspond to instances … how then does a verifier check that these commitments correspond to publicly committed to values ?

Verifier proof slicing

Given that the commitments are the first elements written to the transcript, and that the hypothetical verifier knows the number of values being committed to, the verification process is thus:

• Given a set of public commitments the verifier recreates a transcript consisting solely of the publicly committed to values, creating a transcript of N bytes.
• Upon receiving a proof, the verifier then swaps out the N first proof bytes for the verifier’s transcript bytes.
• Verification then proceeds as usual.

Again if you like rust code:

 // kzg commitments are the first set of points in the proof, this we'll always be the first set of advice
for commit in commitments {
    transcript_new
            .write_point(*commit)
            .map_err(|_| "failed to write point")?;
    }

let proof_first_bytes = transcript_new.finalize();

snark_new.proof[..proof_first_bytes.len()].copy_from_slice(&proof_first_bytes);

If the verifier or data provider needs to generate the commitments themselves, given some pre-image, this can easily be done using ezkl and only require access to the verifying key and the public SRS (if using KZG commitments).

How can I use this today

You can already use this in ezkl and we have an example for doing so here:

If you’re using the cli, all it requires is setting the kzgcommit visibility on whichever part of the computational graph you want to commit to. For instance if pre-commiting to the settings:

ezkl gen-settings -M network.onnx --param-visibility "kzgcommit"

If you want to publish the commitments you can generate them using:

ezkl gen-witness -D input.json -M network.compiled -V vk.key -P kzg.srs

where -V and -P are optional parameters required to generate the commitments.

Note: the commitments can also be generated standalone using python (see below) as:

# if you want to generate the commitments separately 
ezkl.kzg_commit(message, srs_path, vk_path, settings_path) 

As the verifier you can easily swap the proof bytes for the pre-committed ones as such:

ezkl swap-proof-commitments --proof-path proof.proof -W witness.json

where witness.json is a .json that contains the commitments.

All of these commands have python analogues

run_args = ezkl.PyRunArgs()
# this tells the ezkl compiler to leave the columns corresponding to the parameters unblinded
run_args.param_visibility = "kzgcommit"
ezkl.gen_settings(model_path, settings_path, py_run_args=run_args)

...
# gen commits
ezkl.gen_witness(data_path, compiled_model_path, witness_path, vk_path=vk_path, srs_path=srs_path)

... 

# swap out proof bytes
ezkl.swap_proof_commitments(proof_path, witness_path)


... 

# if you want to generate the commitments separately 
ezkl.kzg_commit(message, srs_path, vk_path, settings_path)