Introduction

Verifiable computation is the notion of proving correctness and security between nodes in network systems. Proof-carrying data (PCD) is an approach to achieving verifiable computation through cryptographic mechanisms.

PCD has been a topic of research for a little more than a decade — if you’re unfamiliar, we suggest checking out the appendix before we discuss our experiments in practically building PCD systems.

Improving PCD Systems

An emerging PCD system is Zupass, created by the PCD team at 0xPARC Foundation. You may have run into Zupass as the ticketing system for Zuzalu, Zuconnect, and Devconnect. Zupass enables users to produce proofs on their mobile devices every time they enter an event. In some cases, every time they change floors.

Beyond ticketing, Zupass serves as an interface for managing private user-controlled data. This itself is a user-centric application on top of the generalizable PCD SDK framework. The framework intends to provide a set of interfaces for reasoning about and processing PCDs. It also intends to support the various types of underlying PCDs.

What do we mean by “various types” of PCDs? There are many options for the type of proofs that the data carries — probabilistic proofs like zkSNARKs, signatures, merkle proofs, hash commitments, keypairs, and beyond. While Zupass can hold many types of PCDs, we observe that the current library of PCD types is limited to simpler proofs like the Semaphore set membership proof. This is because the current implementation uses Circom, which is a general-purpose domain-specific language for building proofs. Circom is effective because it’s low-level, but challenging to write with.

We’ve spent much of our time designing APIs to make proof-writing easier. In particular, we built the EZKL library for straightforward in-program proof generation. Let’s experiment with using EZKL to rewrite the business logic for Zupass. We aim for this to provide foundation for a more extensive set of PCDs available in Zupass.

Rewriting Set Membership

The main PCD in Zupass so far is set membership, which is a proof that a user is included in a larger group.

Traditional set membership associates a given user with a password or leverages an identification system (government IDs, a named concert tickets, membership cards). Though these systems are effective, they reveal fragments of potentially identifying information and as such are by default not private and less secure.

One of the first applications of zkSNARKs was the Sempahore protocol, a set membership system for proving you belong while masking your identity (and more). We can use EZKL to even extend private set membership protocols to encompass a wider range of identity schemes such as vocal and facial recognition. Further, we can build applications that allow for key recovery or private verification of a user’s identity based on biometric data. Some of our users are already working on this.

As a first demonstration of the EZKL x PCD combination, we’ve built a simple set membership system using EZKL and Zupass. We built the EZKL set membership circuit in a few lines of Python code, and use Zupass to display the resulting proof — the process doesn’t require any knowledge of Circom, and can be done entirely in Python and Javascript. We hope that this broadens the community of developers and applications that use zero knowledge proofs.

How it Works

Set Membership Model with Pytorch

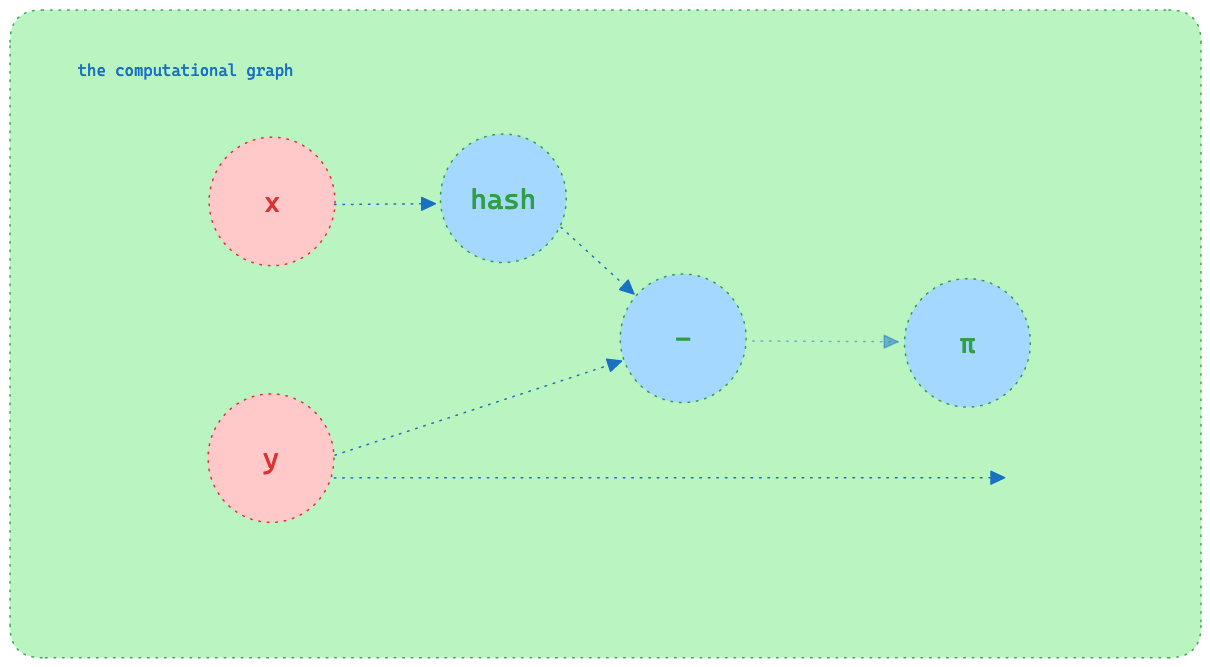
With just a few lines of Pytorch and a few lines of EZKL we can build a set membership system.

class set membershipModel(nn.Module):
    def __init__(self):
        super(set membershipModel, self).__init__()

    def forward(self, individual, members):
        diff = individual - members
        membership_test = torch.prod(diff, dim=1)
        return (membership_test, members)

We define a model that takes two inputs:

• The individual being checked
• The members of the set

We then subtract the individual from each of the members (the set difference). This results in a tensor (array) where each element is the different between individual and each of the members. We then take the product of this tensor to test for the zero product property. That is, the product of the set of numbers is zero if and only if at least one of the numbers in the set is zero.

Therefore, if the individual is a member of the set, the product will be zero. Otherwise, the product will be non-zero.

Consider a trivial example where individual=3 and members=[1,2,3,4]. The set difference will be [1-3,2-3,3-3,4-4]=[-2,-1,0,1], which implies the product will be zero.

Zero Knowledge Circuit with EZKL

In the EZKL config, we design the circuit such that we hash the individual and members with Poseidon (a common hash function) and fix the output to be 0. This means that if the hashed individual is a member of the set, the product will be nil and the fixed output will be satisfied. If the individual is not a member of the set, the product will be non-zero and the fixed output will not be satisfied.

run_args.input_visibility = "hashed/private/0"
run_args.output_visibility = "fixed"

Semantically, we claim that the individual knows or has a pre-image (password), and the hash of that pre-image matches a Poseidon hash that was previously registered to the set as a member. In this way the individual is able to prove they are a member of the set without revealing their identity or the pre-image (password) that hashes to the Poseidon hash.

For the full set of python code see this Colab notebook.

Note 1: This construction is not the most asymptotically efficient construction! We are using an array, linear search, and copy-on-add instead of a tree with efficient insertion and search. However, for small “human-event-sized” sets and where there is large overhead for hashes inside proofs, it can be faster in practice.

Note 2: This scheme is not collision-resistant and does not represent the most secure verification system. We use it here as an intuitive starting point and an easy-to-follow example.

PCD Management with Zupass

We build the application logic into Zupass via the components defined by the PCD interface. The application logic here is simply a registration and login flow, but with PCDs.

We first define two new components:

• Secret Store: the pre-image chosen by the user and set in the system.
• Group Membership PCD: the proof we display as a sequence of QR codes and can verify.

Together, these allow for a Zupass-based application where a user can create a secret pre-image and generate the EZKL proof, and a third-party can verify it – all while keeping the set of members up-to-date and private.

Secret Store

The user provides a pre-image (password), adding the new secret PCD to the user’s Zupass interface. Think of this as personal PCD, which someone can prove is theirs.

The application hashes the pre-image and then registers the resulting Poseidon hash within the set membership server. Once the server rebuilds the set membership model with the new Poseidon hash set, the user is officially a registered member of the set. This might be done at point of sale, or perhaps after verifying another PCD that establishes the right to be included.

Group Membership PCD

When the user wishes to prove they are a member of the set, the Zupass application calls the @ezkljs/engine function prove(). This creates an EZKL proof, which we render as an animated sequence of QR codes.

This is a neat trick for displaying large PCDs. Here, the proof is too large to display in a single QR code. The dynamism means the proof size does not have an upper bound, so it remains practical to use audio or image data as the secret store. This also prevents the user from using a screenshot of the EZKL proof.

Proof Scanner

In practice, a security guard scans the recently generated QR code with the EZKL proof scanner. The scanner picks up each QR code slide and stitches them together into a single EZKL proof.

If the proof is valid, the user is known to be a member of the set! 🎉

There’s more discussion to be had around making this particular example copy-proof, but we omit that here.

Fin!

This experiment is a simple example of how EZKL can be used to build real world prover / verifier systems without having to know a specialized language or framework like Circom, or even interact with a blockchain.

All relevant code can be found in the resources section below.

Beyond simplifying developer experience, EZKL opens the door to a whole new class of applications that leverage AI. For example, you could build a set membership system that uses a voice recognition model to prove you are a member of a set without revealing your identity in the vein of cryptoidol.

We’re excited to see what you build with EZKL, Zupass, and the PCD SDK. If you have any questions or comments, please reach out to us on Discord or Telegram. We’d love to hear from you!

Special Thanks

Special thanks to the 0xPARC team for their work on the PCD SDK and Zupass. Thank you in particular to Gubsheep, Ivan, and Richard for their help in building this demo.

Resources

• Colab notebook for the set membership PCD
• ezkljs engine
• Set membership server
• Zupass fork with new EZKL PCDs

Appendix

What is proof-carrying data?

Proof-carrying data was proposed by Alessandro Chiesa in 2010 as follows.

Proof-carrying data sidesteps the threat of faults and leakage by reasoning about properties of a computation’s output data, regardless of the process that produced it.

In PCD, the system designer prescribes the desired properties of a computation’s outputs.

Corresponding proofs are attached to every message flowing through the system, and are mutually verified by the system’s components. Each such proof attests that the message’s data and all of its history comply with the prescribed properties.

Proof-carrying data is a method where data itself carries a proof of some computation. Think of it like a parcel that comes with a certificate ensuring everything inside is exactly as it should be, according to some predefined rules or computations.

PCD is an approach to achieving a the broader scheme of verifiable computation, which Babai et al. introduced in their 1991 paper on checking computations. The Pinocchio team at Microsoft highlights renewed interest in the early 2010s, given the pervasiveness of cloud computing. Verifiable computation is important in situtations where we outsource computations to a third-party, potentially untrusted worker and seek to verify the correctness of the returned results. Today, this pervasiveness becomes increasingly noticable as we outsource decision making to remote models or forms of articial intelligence.

Network systems already utilize various cryptographic protocols for data transit and handling. Verifiable computation and PCD present a new cryptographic primitive focused on correctness.

The trivial approach to verifying the correctness of a computation is replication. If Alice outsources a computation to Bob, she can prove the correctness of his returned results by simply redoing the computation. However, the trivial approach becomes infeasible when the computation is sufficiently difficult (for example, Bob is running a large ML model). The main advantage of verifiable computation is succinctness, meaning proving / verifying is much less expensive than redoing the computation.

There are many proposed approaches to verifiable computation, and more specifically PCDs. For this piece, we’ve focused on PCDs in the form of zkSNARK proofs (a type of zero knowledge proof) produced by the EZKL library. However, there’s been a number of recent papers proposing PCDs with split accumulation, additive polynomial commitments, arithmetized random oracles, multi-folding schemes, and more. There are also a few implementations of PCD, notably by the arkworks team and the PCD team as in the article.

Another core property of PCDs is that they are transitive: if you pass a PCD to a third party, they should be able to verify the correctness of the computation without further context. This is a powerful property first highlighted by Alessandro Chiesa in his 2010 paper.

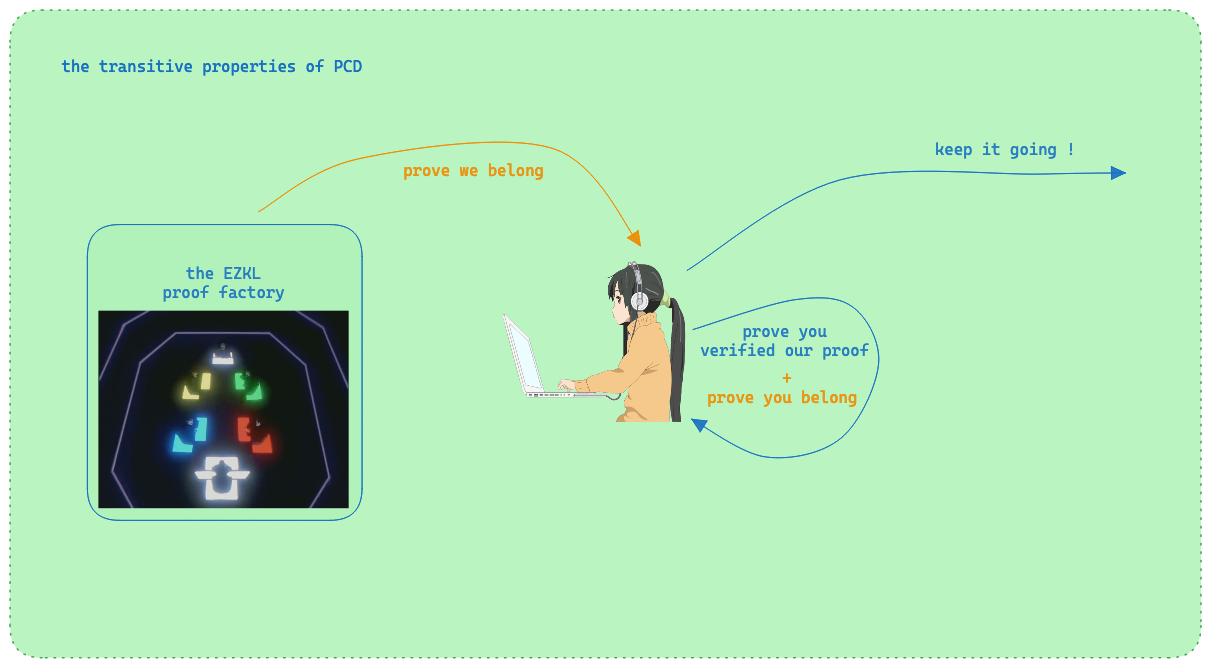
Note: The internet is secured using public key cryptography protocols like TLS and HTTPS. But these protocols are not arbitrarily programmable in the sense that they do not allow for the verification of the correctness of arbitrary computations. Further, transitivity is missing, which is why we need constructions such as TLS Notary.

Isn’t this just blockchain technology?

The astute reader will note that PCDs sound akin to smart contracts, the programmable substrate that underpins blockchains like Ethereum.

While smart contracts offer benefits like data availability and protection against double spending, they also have drawbacks, such as the high cost of achieving consensus. In contrast, PCDs, especially those based on zk proofs, trade-off consensus security for built-in privacy and scalable composability.

What the blockchain ecosystem offered was an incubation environment for practical cryptographic primitives. Recent developments focus on SDKs and APIs for easier transmission and processing of cryptographic data, potentially broadening verifiable computation systems’ applicability beyond blockchain to a wider range of internet applications.

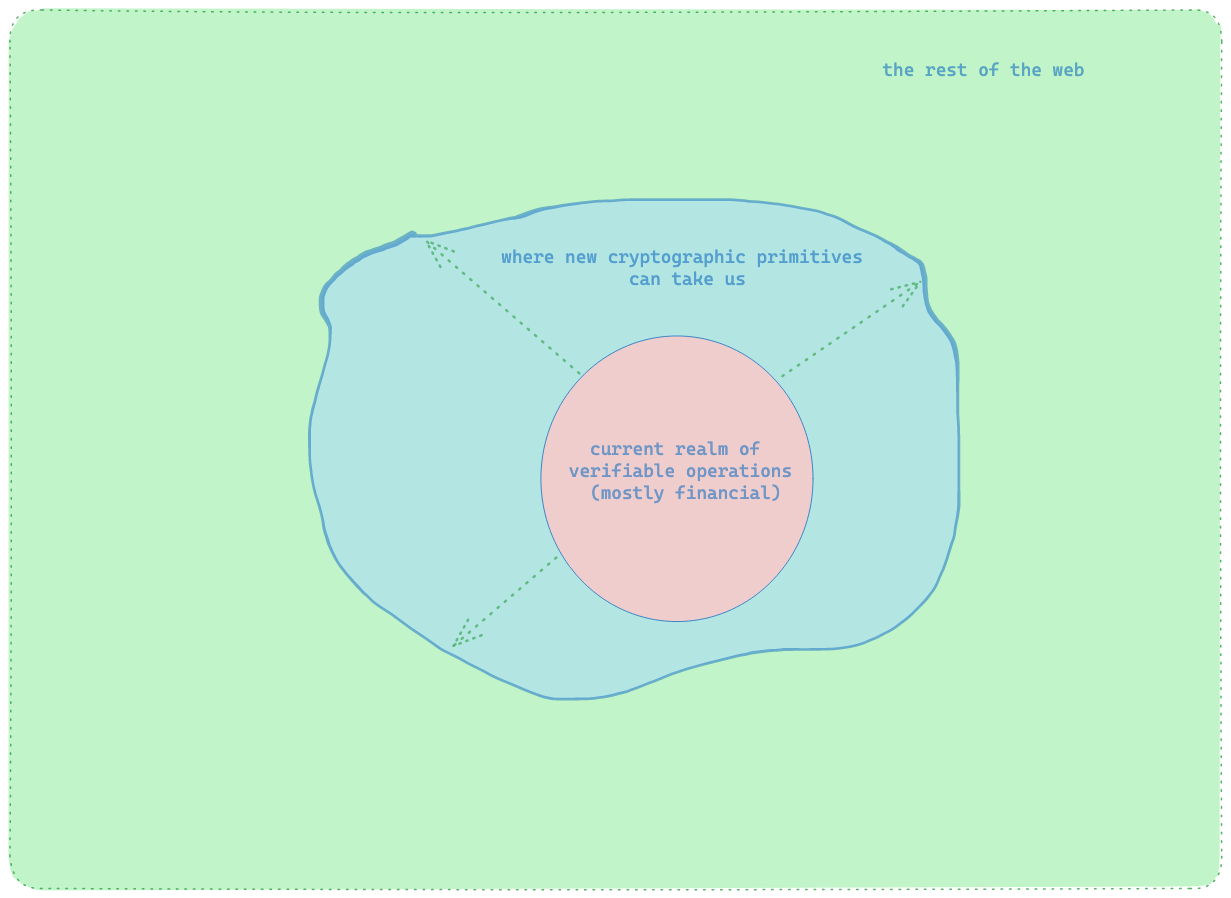
You may notice that many of our tutorials so far have focused on building zero knowledge circuits whose proofs can be verified either in-program or with a verifier contract deployed on an EVM-based blockchain for added security.

Smart contracts as verifiers offers a few advantages:

1. The verifier contract can be deployed once and used to verify an infinite number of proofs, and as such has a one time deployment cost.
2. Verification does not modify the state of the verifier contract, and as such verification is free (if run locally).
3. They offer a canonical source of truth for the verifier code that can’t be post-hoc modified.

However, such verifiers aren’t always best for applications with frequently-changing or large, complex circuits. Blockchain-based verification is useful for peristent security, but it is not a dependency for verifiable computation and PCD.