Splitting and Parallelizing Proofs

In our last post we discussed how to leverage unblinded Advice columns to commit to data in a low overhead manner. In this post we’ll discuss how to leverage these commitments to split a proof into multiple parts.

A natural limitation of most proving systems is that they require all the data to be proven over to be available at the same time. This is because the proving system is designed to generate a single proof over a single set of data and often over a single machine.

This is a limitation we’ve encountered with ezkl. We’ve started to encounter models that handily generate over 200 million constraints. The corresponding circuits these models generate tend to max out most machines’ memory and as such we’d like to be able to split the proof generation process into multiple parts such that either:

  • The proof generation of the split circuit can be parallelized across multiple machines, or
  • The proof generation process can be generated in sequence over these less memory intensive circuits.

Stitching Proofs Together

Say we have two proofs that are generated independently but we want to demonstrate that the values in the second advice column of the first circuit, lets call these the “outputs” of the first circuit, are the same as the values in the first advice column (“inputs”) of the second circuit.

A natural way to do this is to commit to the values in each of these columns, and then to check that the commitments are the same. The Poseidon hash gadget in Halo2, covered here, which would be a good attempt at this, introduces considerable overhead and is not ideal when the values being committed to are high dimensional (eg. large logrows).

A cheaper solution is to use the unblinded advice columns we discussed in the last post. We can commit to the values in the second advice column of the first circuit, and then check that the values in the first advice column of the second circuit are the same using the verifier commitment swaping scheme.

See here for an illustration of this:

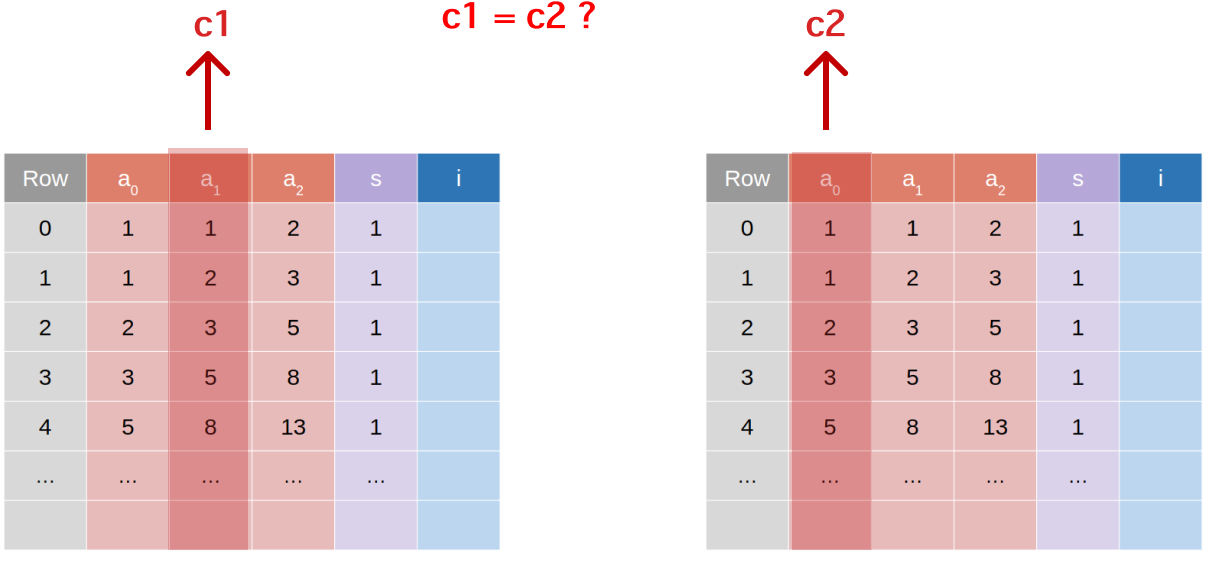
Because the verification of commitment matching between circuits happens at the verification step and not at the proof generation step, we can split the proof generation process into multiple parts and execute the proofs asynchronously.

Note: This could also be done with instances but if the stitching happens on-chain, this becomes prohibitively expensive for large circuits. The kzg-commits are already included in the proof transcript, so we might as well use them. Further the kzg-commits, if they change at every proof generation, maintain pretty good privacy properties. See our previous post for notes on this.

The next section is a brief refresh on how the verifier commitment swapping scheme works in Halo2. If you’re familiar with this you can skip to the section on how to leverage this scheme to split proofs.

Refresher: To avoid having to do complex indexing later on, we put the values that are being committed to in the first columns of the plonk grid. Say we’re committing to 3 separate datum, D1,D2,D3 we’ll want to assign each of these to the rows of the unblinded advice a1,a2,a3. 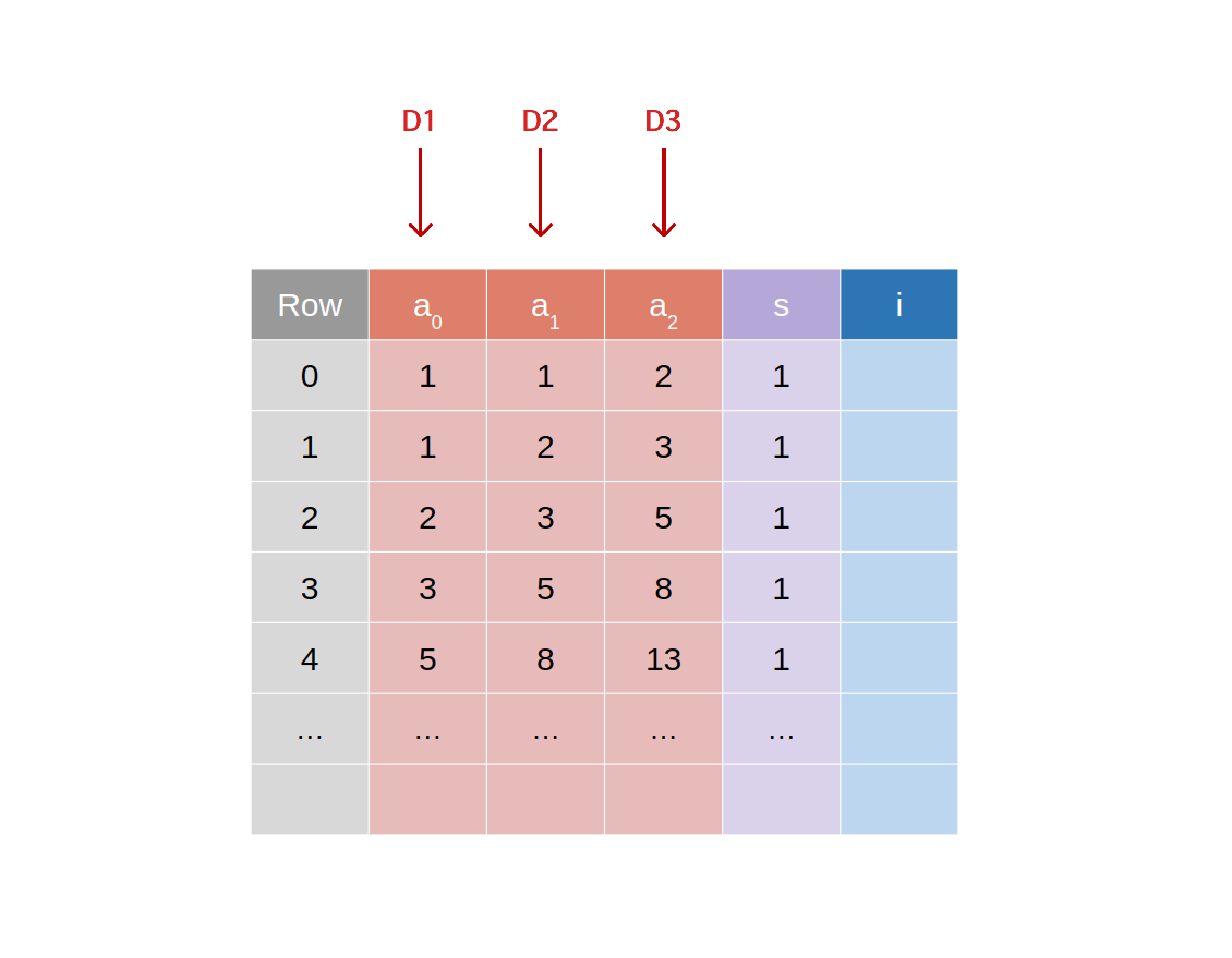The proof transcript is then generated and the affine projections of the curve points that correspond to the commitments to D1,D2,D3 are its first elements. Given that the commitments are the first elements written to the transcript, upon receiving a proof, the verifier then swaps out the N first proof bytes for the verifier’s transcript bytes. Verification then proceeds as usual.

Splitting Proofs

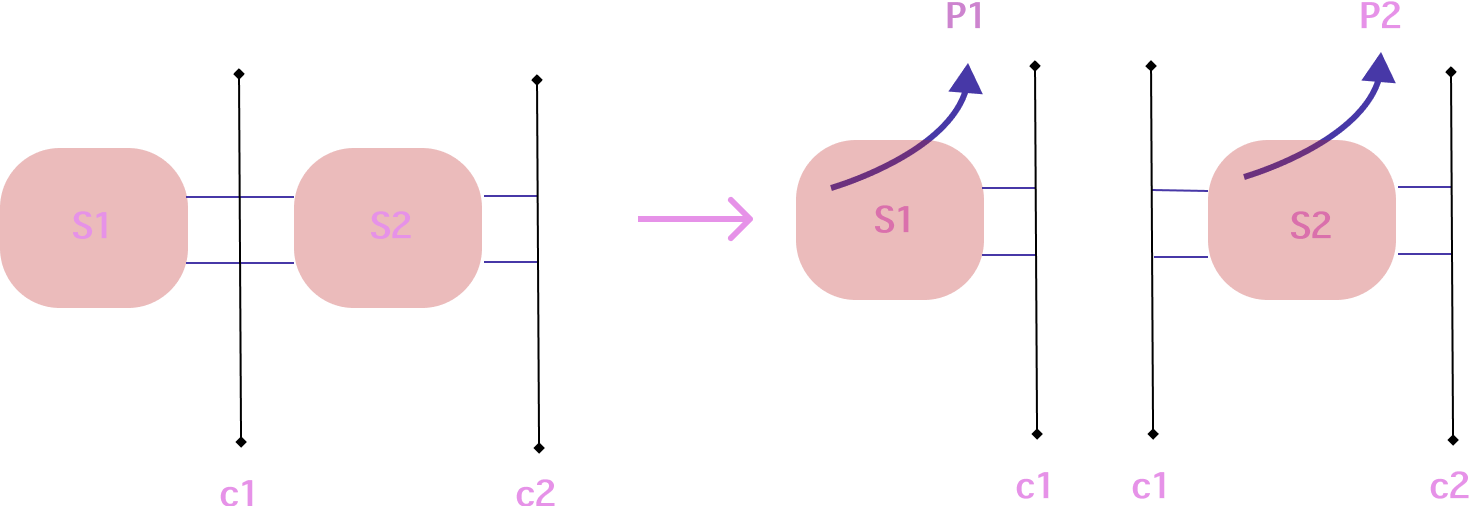
The verifier commitment swapping scheme can be leveraged to split proofs in the following manner. Steps that are parallelizable are marked with an ♾️.

  1. ♾️ Given a circuit S we partition it into N non-overlapping circuits of constraints S1,S2,...,SN, each with the same K logrows.
  2. ♾️ For each of these we generate a corresponding proving key pk1,pk2,...,pkN and a corresponding verifying key vk1,vk2,...,vkN.
  3. We can then generate the expected commitments for the “input” and “output” columns that should match in sequence. This can be done simply with a witness generating pass that doesn’t generate a proof. In this case the “output” columns of Ci are the “input” columns of Ci+1.
  4. ♾️ We then generate the proofs for each of these circuits yielding P1,P2,...,PN.

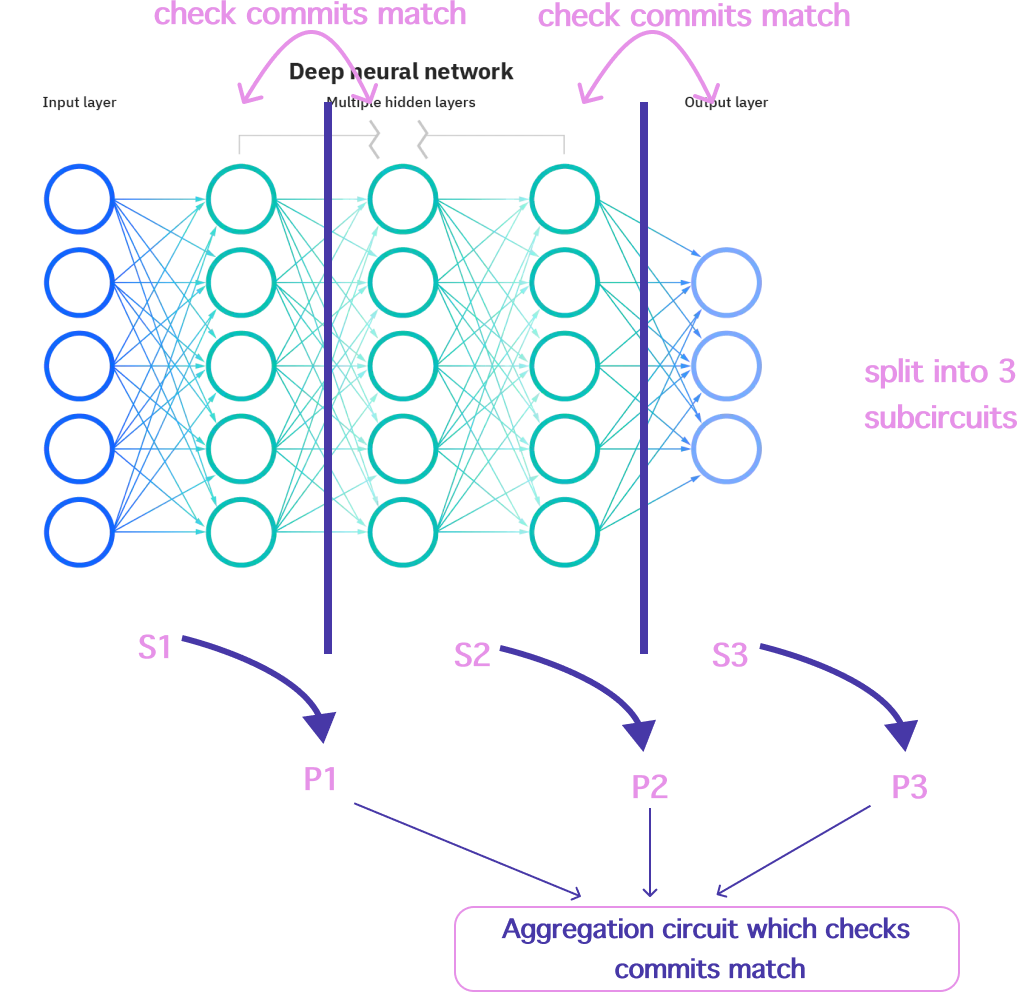
On the verifier side:

  1. ♾️ For a given proof Pi we can then swap out the first set of commitments for the corresponding commitments in Pi-1.
  2. ♾️ We then verify each proof Pi.

Note that this verification can also be performed using PSE’s aggregation circuit to aggregate the proofs into a single proof. This is a good option if the verifier is on-chain and the cost of verification for multiple split proofs is high. We provide the option to do this in ezkl, with a single boolean flag split-proofs in the aggregation related commands. This ensures the circuit also constrains the unblinded proofs “inputs” and “output” to match in sequence.

In python for instance this would look like:

# now mock aggregate the proofs
proofs = []
for i in range(3):
    proof_path = os.path.join('proof_split_'+str(i)+'.json')
    proofs.append(proof_path)

ezkl.mock_aggregate(proofs, logrows=23, split_proofs = True)

The demos below show how to leverage this.

How can I use this today?

You can already leverage this in ezkl today ! We have examples showing how to split proofs for

  • a simple conv network Notebook

  • a gan network Notebook